C++ Bc. 29: Porovnání verzí

Aktuální verze z 10. 10. 2006, 14:16

Metoda tětiv (regula falsi)

Pro spojitou funkci $f(x)$ , která v krajních bodech intervalu $(a,b)$ nabývá různých znamének, tj. platí $f(a)f(b)<0$ , má v tomto intervalu rovnice $f(x)=0$ alespoň jeden reálný kořen.

Numerická iterační metoda regula falsi hledá jeden z kořenů rovnice $f(x)=0$ tak, že křivku $f(x)$ nahradí v daném intervalu přímkou a její průsečík s osou $x$ je $i$ -tým odhadem kořene

$x={af(b)-bf(a) \over f(b)-f(a)}$

Podle znaménka $f(x)$ nahradí jeden z krajních bodů intervalu $(a,b)$ odhadem $x$ .

Pro zadanou toleranci t je výpočet ukončen, pokud je $|a-b|<t$ nebo $|f(x)|<t$ .

Napište funkci, která implementuje metodu tětiv. Parametry jsou ukazatel na funkci, hodnoty intervalu $(a,b)$ a volitelná hodnota tolerance. Funkce kontroluje, zda je splněna podmínka $f(a)f(b)<0$ a vyvolá výjimku Chyba, pokud je zadán interval ve kterém není zaručena existence kořene.

typedef double (*Funkce)(double);
double tetivy(Funkce f, double a, double b, double tol=1e-12);

Příklad

Odhad jednoho z kořenů funkce $y=\sin(4x^{2}-x-0.3)$ .

Aproximace korene x = 0.42604    f(x) = -1.52884e-13

[ Zpět | C++ | Další ]

@@ Řádek 1: / Řádek 1: @@
+;[http://en.wikipedia.org/wiki/Regula_falsi Metoda tětiv (regula falsi)]
+Pro spojitou funkci <math>f(x)</math>, která v krajních bodech intervalu <math>(a, b)</math> nabývá různých znamének, tj. platí <math>f(a)f(b) < 0</math>, má v tomto intervalu rovnice <math>f(x)=0</math> alespoň jeden reálný kořen.
+Numerická iterační metoda ''regula falsi'' hledá jeden z kořenů rovnice <math>f(x)=0</math> tak, že křivku <math>f(x)</math> nahradí v daném intervalu přímkou a její průsečík s osou <math>x</math> je <math>i</math>-tým odhadem kořene
+<math>x = {a f(b) - b f(a) \over f(b) - f(a)} </math>
+Podle znaménka <math>f(x)</math> nahradí jeden z krajních bodů intervalu <math>(a, b)</math> odhadem <math>x</math>.
+Pro zadanou toleranci ''t'' je výpočet ukončen, pokud je <math>|a - b| <   t</math> nebo <math>|f(x)|<t</math>.
+Napište funkci, která implementuje metodu tětiv. Parametry jsou ukazatel na funkci, hodnoty intervalu <math>(a, b)</math> a volitelná hodnota tolerance. Funkce kontroluje, zda je splněna podmínka <math>f(a)f(b) < 0</math> a vyvolá výjimku [[C++ Bc. Chyba|Chyba]], pokud je zadán interval ve kterém není zaručena existence kořene.
+ typedef double (*Funkce)(double);
+ double tetivy(Funkce f, double a, double b, double tol=1e-12);
+'''Příklad'''
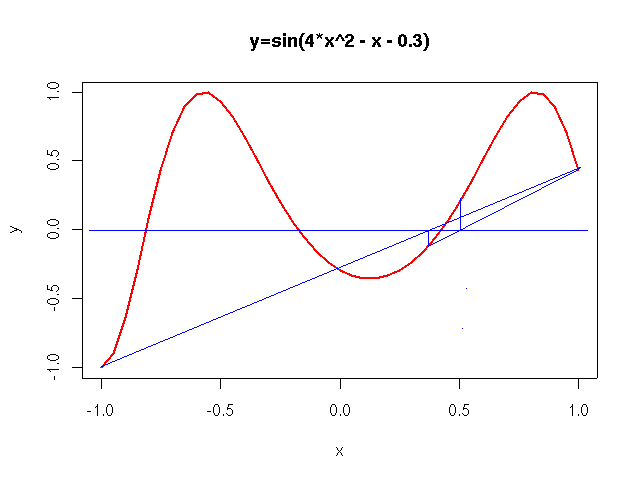
+Odhad jednoho z kořenů funkce <math>y = \sin(4x^2 - x - 0.3)</math>.
+ Aproximace korene x = 0.42604    f(x) = -1.52884e-13
 <!-- [[Soubor:C_plus_plus_Bc._29.png|center|frame|Obrázek: Průběh funkce '''y = sin(4*x^2 - x - 0.3''']] -->
 [[Soubor:C_plus_plus_Bc._29.png|center|frame]]
-[ [[C plus plus Bc.|Zpět]] | [[C plus plus Bc. 29 cpp | C++ ]] ]
+[ [[C++ Bc.|Zpět]] | [[C++ Bc. 29 cpp | C++ ]] | [[C++ Bc. 30|Další]] ]
+[[Kategorie:Programování]]